 |
| http://www.themathpage.com/acalc/calc_IMG/042.gif |
| http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG |
Where does the formula of difference quotient come from?
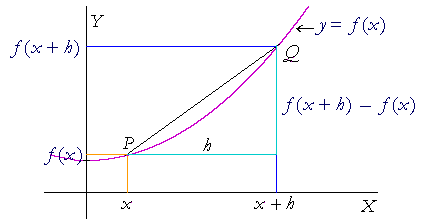
We are shown in these graphs a visual to where the difference quotient came from. We know that from one part to the other it is x. Which means that is we increase the length it would be known as x+h. We must remember that x and h are just variables they can be changed but these are just some that we prefer using since thy appear on the difference quotient. These variables can be used interchangeably doesn't always have to be x and h. The y-values would be f(x) meaning that the point is (x,f(x)) and f(x+h) which means are point is (x+h, f(x+h)). We want to find the slope of these two points in order to be able to find the distance between them. In order to find the slope we use the slope formula being Ysub2- ysub1 all divided by Xsub2 minus Xsub1. Once we plug in all these numbers in we get f(x+h)-f(x) / x+h-x. If we simplify this the x on the denominator will cancel out giving us the difference quotient equation known as f(x+h)-f(x)/h. This can be used in order "to find the slope of a function at a single point". (google)
resources: Mrs. Kirch
https://www.youtube.com/watch?v=XA0fZh8cXV8
This video helps demonstrate exactly what i was referring to above but provides a greater visual as to where the difference quotient comes from. Demonstrates that the difference quotient can be derived using any function. Also, showing that it all starts from the slope formula and how it is used to find the "slope of a function as a single point."