2. Algebraic Equation:
(X-h)^2/a^2 + (y-k)^2/b^2=1 (horizontal)
(x-h)^2/b^2 + -k)^2/a^2=1 (vertical)
(http://theo.x10hosting.com/examples/Ellipse/Ellipse7.jpg)
There are some very important key parts that an ellipse contains which are what defines it. There is a major axis, minor axis, foci and co-foci, vertices, and a center. These components are the components of an ellipse.
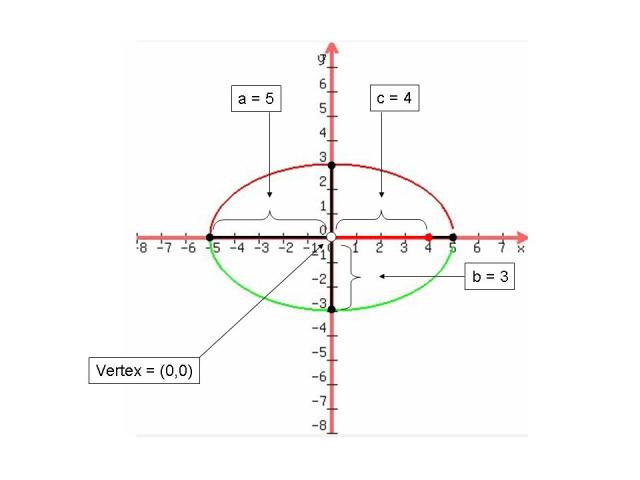
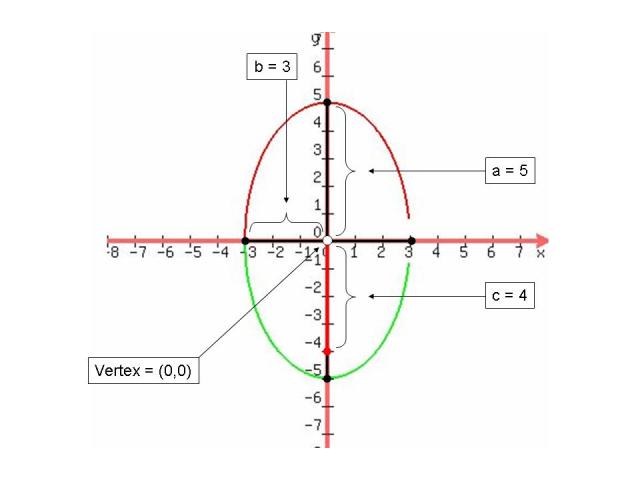
As we can see the graphs vary depending on where the greater value is. a must be the value of the greatest denominator. We see that the further away the foci is from the end point the skinnier the graph gets. The closer the foci is from the end point the skinnier the graph gets. The foci always lies under the major axis.
For more information on Ellipses see click this link http://www.purplemath.com/modules/ellipse.htm
#4 Real World Application: There are various components to Form an Ellipse. The standard form of an ellipse must have a plus sign in between the two terms and must be set equal to 1.To find out if the graph will be fat or skinny then we have to see what the transverse axis is, if the greater number is under "x" then it will be a fat ellipse of the grater number is under "y" then it will be a skinny ellipse. The transverse axis is equal to 2a which is the measure from one vertice to the other. To find "a" we take the distance between the center and one vertice. The Major axis contains "a", "c" and The center. The minor axis contains "b" and the center. To find "b" we know that it is the distance between one co-vertice to the center. To find the eccentricity of an ellipse we use c/a which should be 0>e<1.
(http://t0.gstatic.com/images?q=tbn:ANd9GcSrxcN_F6b6JjbiOJo-VBDHOTMXGdT_Ddr9Arm8kSI8VXNSRz2s8oc5ltfl)
This is a demonstration as to how ellipsis apply to the real world. The orbit of the planets consists of elliptical orbits. The sun is used as the center of the ellipse that all the planets have. The further away from the planet is the greater its foci will be. In order for everythibg to stay in balance tge eccentricity of each ellipse should be greater than 0 but les than one. The orbit of the planets must be in this shape or else the elements will be unbablanced which will
Video:This demonstrates the shape tgat the earth goea around using the un to be its point of orbitibg. The planets go around the sun so it serves as their main focus to help them stay balanced. The position of the sun depends on which planet is orbiting. However the the sun if the part that all the planets revolve around just like the center would be for an ellipse.
#4 Work cited
google.com
youtube.com
kirchmathanalysis.blogspot.com
wikipedia.org

No comments:
Post a Comment