BQ#4: Unit T Concept 3: Tangent and Cotangent Differences

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill? 

 Tangent Graph                                                                                                     Cotangent Graph

We see on the graphs that there are 4 colors that show different sections. The red represents the first quadrant, green represents the second quadrant, orange represents the third quadrant, and blue represents the fourth quadrant. When we are graphing tangent we look at the pattern that is being placed. which would be positive, negative, positive, negative since that is what they are on the unit circle. Asymptotes are formed whenever we have an undefined answer and on the graph an undefined answer would be on pi/2, 3pi/2. The order in which we graph would be positive, asymptote cutting the graph, negative, positive, another asymptote splitting the graph, and negative. Creating an uphill graph is we only look at one period. 

For cotangent in there are undefined answer would be in 0, pi, 2pi. The graph would be positive to negative attached then it would break because of the asymptote creating an downhill graph. If we compare the two graphs of a tangent and we see that the asymptotes are placed on a different spot changing the pattern of the graph from uphill to downhill. Depending on where the asyptotes are located of the graph it will change the way that it looks because asymptotes serve as a wall barrier that does not allow the graph to go through it. 

BQ#3: Unit T Concepts 1-3- Relation Between Sine and Cosine on Other Trig Graphs

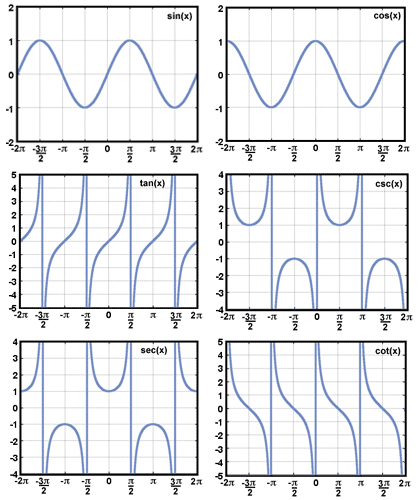
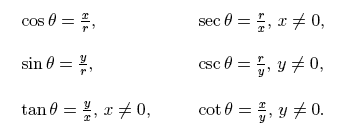How do the graphs of Sine and Cosine relate to each of the others? 

If we think about how all the Trig functions relate to sine and cosine we will see a connection. The rest of the functions have some sort of relation that has sine or cosine in it. 

a)

Tangent with cosine and sine 

We know that tangent is equal to the trig function of sin over cosine. We have to see what will make this function undefined. The only way for it to be undefined is by having cosine equal 0. If the function is undefined we see that an asymptote is being created, not letting the graph touch or go through that asymptote it serves as a wall. We see on the graph that whenever the cosine graph is on the x axis with the value of zero there is a break on the tangent graph demonstrating the placement of the asymptote. 

b)

cotangent with sine and cosine 

The trig function for cotangent is cosine over sine. If we want to check for asymptotes we have to see where on the graph this would be true in which sine will equal 0. Sine is equal to 0 in 0, pi and 2pi. Whenever sine equals 0 on the graph we see that there is a break that cotangent cannot touch representing the asymptote. We can also see the relation between tan and cot they are faced the opposite way one is uphill the other downhill and that is because of the other and place that the asymptotes are at because 

C)

Secant with Cosine

The trig function of secant is r/cosine. "r" stands for 1 since we are using the values of the unit circle. So this means that the trig function is 1/cosine. In order to have asymptotes there must be a place on the graph that will make this function undefined. The only way for it to be undefined is by having cosine equal 0. On the unit circle unit circle cosine =0 on pi/2 and 3pi/2. This means that there will be an asymptote there. If we look at the graph we see that where ever cosine is on the x axis with a value of 0 then the graph for secant splits. This split represent the asymptote that cannot be touched.

d)

Cosecant and sine

The trig function for cosecant is r/sine. When we are talking about the unit circle the radius is one making the function just 1/sine. To find the asymptotes we have to see in which part of the graph will it be undefined making sine=0. In the Unit circle sine is 0 at 0, pi,  and 2pi. 0 is the start of the period that we are looking at and 2pi is the end which means that there is one asymptote in between being pi. If we see the graph of sine we see that the graph lands on the value of 0 on the x axis on the same points creating the asymptotes that separate the graph for cosecant making this impossible for the graph of cosecant to touch because of it. We draw the u shapes on the hump of the sine graph put it facing up if it is above the x axis and face down if it is below. 

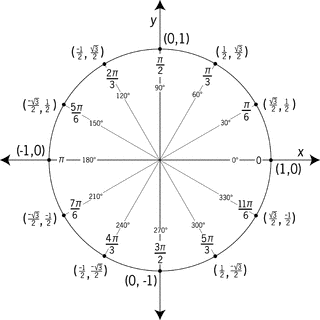
The direction in which the hump is going( above or below the x-axis) depends on ASTC. On what the value will end up being on each quadrant.

In Cooperation with desmos.com created by Mrs. Kirch

BQ#5: Unit T Concepts 1-3: Reason why Sine and Cosine Do not have Asymptotes

http://www.biology.arizona.edu/biomath/tutorials/trigonometric/graphics/trigbasiceqna.gif

Why do sine and cosine not have asymptotes? 
Asymptotes are formed when the answer is undefined. If we see the trig functions and what they are for sine and cosine we see that the ratio for sine is y/r and x/r. In order for these graphs to have asymptotes the ratio must me undefined. This means that they must be divided by 0 but r=1 so this will not happen because in the unit circle r is always 1. 

Why do the other trig functions have asymptotes?
The other trig functions do have asymptotes because they can be undefined in certain parts because of its ratio. We see that cosecant is r/y. If y is equal to 0 then the graph will have asymptotes when ever the ration is undefined creating an asymptote. Secant has a ration of r/x is whenever x=0 there will be an asymptote since it will be undefined. In Tangent we have a ratio of y/x if x=0 then the answer will be undefined creating an asymptote. Cotangent x/y if y=0 then it will be an undefined ratio creating an asymptote. The trig functions that have the same asymptotes are secant and tangent because they have the same denominator of x and cotangent and cosecant will have the same asymptotes because they have a denominator of y.  

with cooperation with Google.com

BQ #3: Unit T concepts 1-3: Relating the Trig graphs to the Unit Circle

How do trig Graphs relate to the Unit Circle? 

http://etc.usf.edu/clipart/43200/43217/unit-circle9_43217_md.gif
http://img.sparknotes.com/figures/A/ad79275cb59e569b790cb945a4ffc553/triggraphs.gif

The Trig Graphs relate to the unit circle because they are originated from it in which they have been unraveled from being a circle. These trig graphs follow the same patterns as the unit circle except that they are not in a circle form more like waves. The coordinates are still the same and have the same positive and negative signs there on the trig graph. (a) A period is how long it takes in order for the cycle to repeat its pattern. The period or sine and cosine is 2pi because that is how long it takes the graph to repeat its pattern. The pattern for sine is positive, positive, negative, negative, which comes from the unit circle using ASTC. The same thing is being applies there. The Pattern for cosine is positive, negative, negative, positive, also comes from the ASTC on the Unit Circle. The reason why tangent and cotangent have a period of pi is because that is how long it takes for the cycle to be repeated the pattern being positive, negative, positive negative throughout the unit circle. The positive negative is the pattern and it is being repeated twice in one revolution of the unit circle half of 2pi is pi which is why tan and cot have a period of pi. (b) Amplitude also has a relates with the trig graphs and the Unit Circle. The Amplitude is half the distance between the highest and lowest points of the graph. In the Unit Circle sine and cosine cannot be greater than or equal to 1 or -1. With this being said those are the restrictions that are set upon those two functions. The other trig functions don't have amplitudes because because they do not have any restrictions on the Unitt Circle since tan and cot can be greater than 1 or less than -1. 

In the trig graphs they are divided in 4 sections which are the quadrants when they are put into Unit circle Form. This guides whether the graph will be going above or below the x axis. If it is above the axis than the function was positive in that quadrant, if the hump is \ the axis then the function was negative on that quadrant. 

In Cooperation with google.com

Reflection #1 Unit Q: Verifying Trig Identities

1. What does it actually mean to verify a trig identity?
When we verify a trig identity this means that we are proving that this trig identity always true. This identity should always be true no matter what is plugged into it if it is used with its rightful pair. sec and tan go together which means that they can turn into each other back and forth with the edition of the one.Since sec^2x - tan^2x= 1. This can be arranged in all sorts of ways and it will be true since it is and identity meaning that is has been proven that this equation will always work. Cos and Sin go together making cos^2x + sin^2 = 1 and it too can be arranged into different forms and it will always be true because these identities have been verified that it works. Cot and csc go together making 1+ cot^2x= csc^2x. All these identities have been verified that they are true and that will always work if they are being used in the correct form.

2. Tips and tricks i have found helpful.
Some tips and tricks that we can use in order to simplify or solve trig equations are that we can always check for a GCF( greatest common factor), conjugate, breaking down fractions that are monomials, factoring, foiling, and substitution of identities. (Kirch SSS packet). If you are completely stuck you can always change everything in terms of sin and cos. Most of the time if there is a potential way to make and identity or to form one that is the path i decide to take. The reason being that this usually tends to cancel with something else or it can become the one trig function that is left to use. When we see that we have a binomial either in the numerator or the denominator and there is no given identity then we can always multiply by a conjugate. This will help us get squares and lead us to finding an identity. When we choose to factor is is because we have either the same base or because we have multiples of 2 on our exponent. When we foil is because we  know that there is a possibilities that we may get squares making that a potential identity that can simplify to something else. The reason why we decide to change everything to sin and cos if we are completely stuck is to see if there is a different rout that we end up checking and work away around it.

3. Verifying a trig function 
To verify a trig function it means that we are not allowed to touch the second part of the equal sign. What we are trying to do is make sure that this is valid and will somehow transform into that on the other side. There are multiple ways of being able to verify this but they all have to tie back to the one that is on the other side. The side that we shall always work is usually the more complicated side. When we verify a trig function we state that this is right and that somehow it will turn to what was given to us, giving us a true statement. The first thing that we can try to look at is see what we can do to change the complicated side into the trig function(s) that are listed on the other side of the equal sign. We do this by seeing if there is a GCF that will factor out, if there is and identity. If these are not there then we go to our other options being foiling which i would only use if there are to trig functions that could become and identity if they were being squared. The next option would be finding the least common multiple which would be used if we have fractions that we would like to combine together. Our next option would be using the conjugate this would be used if we have a binomial either on the numerator of on the denominator and we would foil this out. Our last option would be change everything to sin and cos. This is mostly used if you cannot find any other way to verify the trig function in other to make it the same as what is on the other side of the parenthesis. There are times where you feel like that is all you can do in terms of simplifying the answer and it is just not the answer that is on the other side. See if you can break it down if it is a fraction, or see if there is any other way that it can be addressed using  ratio identities or reciprocal identities.  If you don't get it on your first attempt keep trying because there are multiply ways of verifying a trig function, you will eventually get there. :)