http://www.biology.arizona.edu/biomath/tutorials/trigonometric/graphics/trigbasiceqna.gif
Why do sine and cosine not have asymptotes?
Asymptotes are formed when the answer is undefined. If we see the trig functions and what they are for sine and cosine we see that the ratio for sine is y/r and x/r. In order for these graphs to have asymptotes the ratio must me undefined. This means that they must be divided by 0 but r=1 so this will not happen because in the unit circle r is always 1.
Why do the other trig functions have asymptotes?
The other trig functions do have asymptotes because they can be undefined in certain parts because of its ratio. We see that cosecant is r/y. If y is equal to 0 then the graph will have asymptotes when ever the ration is undefined creating an asymptote. Secant has a ration of r/x is whenever x=0 there will be an asymptote since it will be undefined. In Tangent we have a ratio of y/x if x=0 then the answer will be undefined creating an asymptote. Cotangent x/y if y=0 then it will be an undefined ratio creating an asymptote. The trig functions that have the same asymptotes are secant and tangent because they have the same denominator of x and cotangent and cosecant will have the same asymptotes because they have a denominator of y.
with cooperation with Google.com
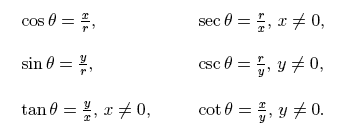
No comments:
Post a Comment