1. What is continuity? What is discontinuity?
 |
http://upload.wikimedia.org/wikipedia/commons/e/e6/Discontinuity_jump.eps.pngJUMP |
 |
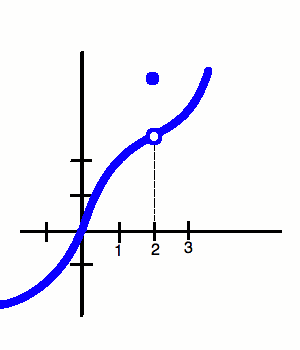
| Google.com http://www.milefoot.com/math/calculus/limits/images/hole1.gif Point |
 |
http://www.milefoot.com/math/calculus/limits/images/oscdisc.gifOscillating |
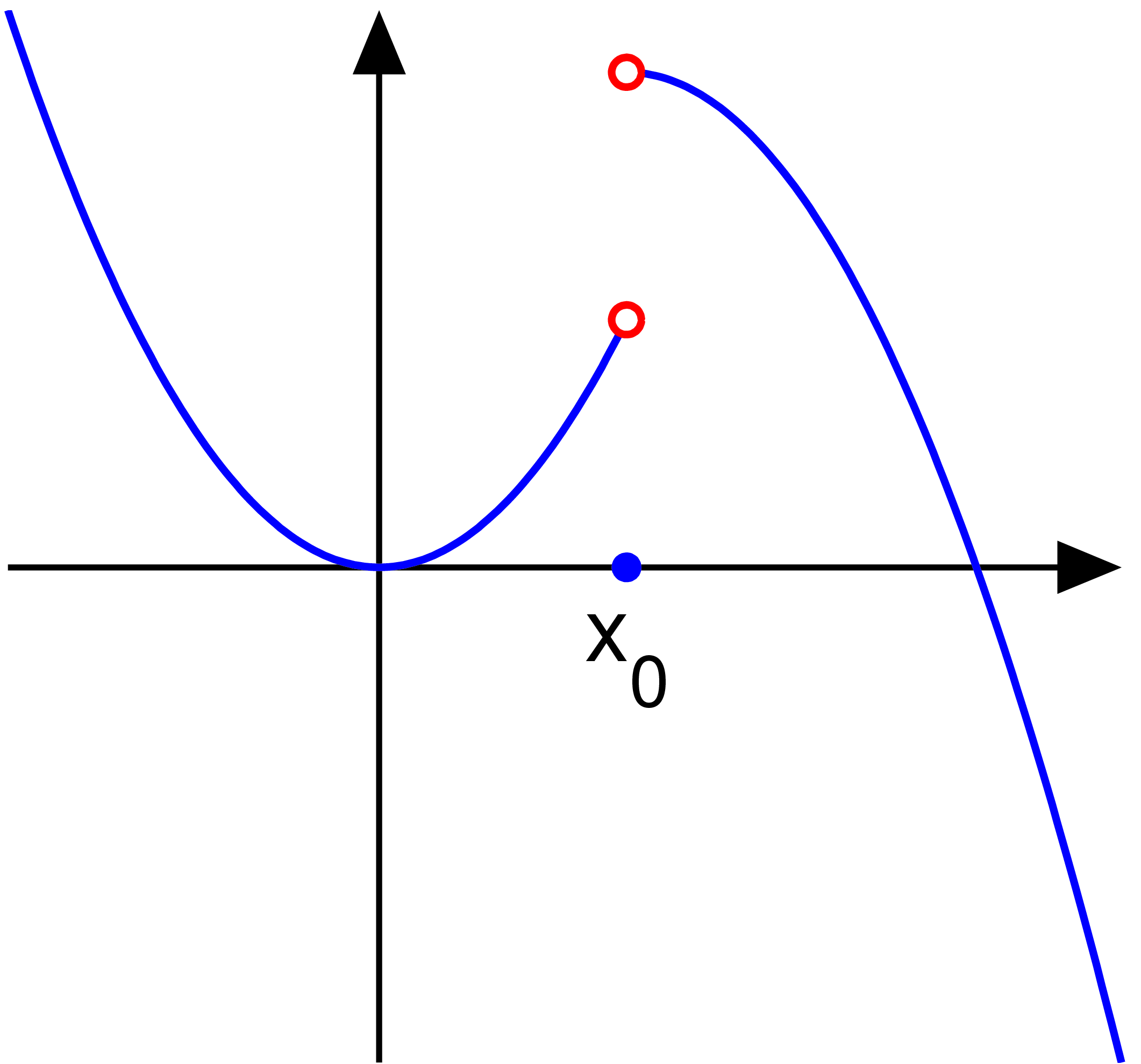
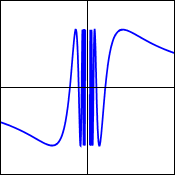
A continuous graph is predictable, has no breaks, no jumps and no holes. You can draw it without lifting up your pencil. There are two groups of discontinuities which are removable and non-removable. In the non removable group there is a point discontinuity known as a hole. In the non-removable group there is Jump which has different left/right limits, Oscillating which is wiggly, and infinite which has a vertical asymptote that leads to unbounded behavior. A discontinuous function is the opposite of a continuous because it cannot be drawn without lifting up your pencil, it is not predictable, it can have breaks, jumps and holes. The reason why a discontinuous function is separated into two groups is because in a removable discontinuity there is always a limit but in the non-removable there is no limit.
 |
http://web.cs.du.edu/~rjudd/calculus/calc1/notes/dis4.pngInfinite |
2.What is a limit? When does a limit exist? When does the limit not exist? What is the difference between a limit and a value?
 |
Limit does exist same L/R approachGoogle.com |
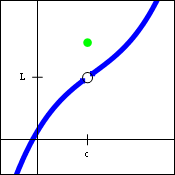
A limit is the functions intended height at a given point. This does not mean that the point that it was intended to reach was actually reached. A limit exist when ever both the left and right meet at the same intended height. However, that does not mean that it equals the same value as the limit. A limit does not exist whenever there is a different left/ right approach. This means that there has been either a jump discontinuity, its oscillating or it is an infinite discontinuity since these do not have a limit. The difference between a limit and a value is that a limit is the intended height, the point does not actually have to be part of the graph in order to be a limit. For a value it has to be the dark circle the point that is actually part of the function, it does not matter if it is not a limit the exactitude is what matters, the actual point.
3. How do we evaluate limits numerically, graphically and algebraically?
 |
| Numerically Google.com |
 |
| Graph Google.com |
Algebraically (substitution)
Google.com
We evaluate limits numerically by using a chart. This chart helps us display what is closer to the number that we want to get to. On the far left we subtract 1 tenth and just make it closer and closer to the number in the middle, on the far right we add 1 tenth and get it closer and closer to the number we want. This helps demonstrate how the closer we get to the left or right of the function we get very very very close to the number in the center. in order to find the y values then we plug in the x-values into the function. Once we get all the y-values then we end up numbers that will lead to a middle number that will make it closer and closer to that middle number. We evaluate the function graphically by placing one finger on the left and the other on the right. We gear our fingers closer and closer to the number of the x-axis that is being asked to find the limit for if they meet then there is a limit if they don't meet there is no limit since there would be a different L/R. We evaluate the limit of a function algebraically by first checking is substitution works. Substitution should be our first options if we get a numerical answer- we are done, 0/#-we are done, #/0 undefined- we are done, 0/0- indeterminate use another method. The next method would be rationalizing/ conjugate method just depends on how the problem looks like, if something could be taken out by factoring then the factoring method would be the next option. These last two methods can be used in which ever order but substitution is always first, since it is the easiest method and will give us the answer faster. Once we have factored out something then we substitute the number in to the remaining equation and that will be our answer. When we do the conjugate we can get the conjugate from either the top or bottom just depending on where the square root is. Once we have simplified then we do direct substitution again. SUBSTITUTION should always be the FIRST option.


No comments:
Post a Comment